座標系

このドキュメントでは、3Dモデルの配置に関連する座標系について説明します。

表記について
このドキュメントでは、 $(x, y, z)$ が (赤, 緑, 青) に対応するように記述します。

1. モデルの表示に関連する座標系

1.1. 各種3Dモデルエディタでの座標系

各種3Dモデルエディタごとに、x軸、y軸、z軸の向いている方向は異なります。例としてBlenderでは、通常下記のように正面が -y軸 方向となるようにモデルを作成します。

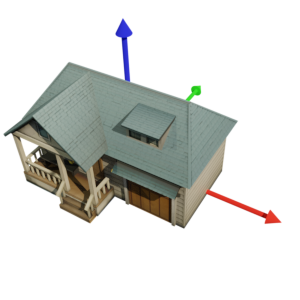
1.2. glTF座標系

Maprayでは3Dモデルのファイル形式としてglTF形式を読み込むことができます。glTFの座標系は Y Up （y軸が上方向）で出力されることが多く、Maprayでもこの座標系で出力されていることを前提に処理を行います。出力されたファイルでは、下図のようにy軸が高さ方向、z軸が正面となるような座標系となります（正面である必要はありませんが本文書では正面とします）。

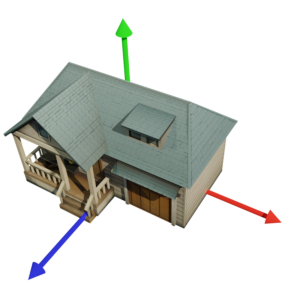
1.3. Maprayでの表示方向

下図は上記モデルをMaprayで読み込んだ結果です。外側・内側の座標系が表示されていますが、外側に表示されている座標系が上記glTFモデルの座標系です。 Roll, Tilt Headingなど、姿勢を制御するパラメータを指定しない場合、3Dモデルは図のような方向に配置されます。 y軸が高さ方向、z軸が北方向、x軸が西方向を向いています（3Dモデルの正面が北を向くことになります）。

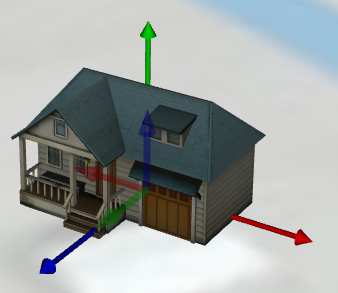
Maprayでは、3Dモデルの方向をMaprayローカル座標系（上図中の内側の座標系）で管理します。

1.4. 3Dモデルの座標変換

Maprayで表現される3Dモデルは、Maprayローカル座標系への変換行列 $T_\mathrm{MLOCS}$ および、姿勢変換行列 $T_\mathrm{attitude}$ が適用されます。全体を通した変換行列 $T_\mathrm{all}$ は下記のようになります。

$\begin{equation} T_\mathrm{all} = T_\mathrm{MLOCS} T_\mathrm{attitude} \end{equation}$

モデルに含まれる点 $\vec{p}_m$ と実際に表示される位置 $\vec{p}_g$ の関係は下記のように計算されます。

$\begin{equation} \vec{p}_g = T_\mathrm{all} \vec{p}_m \end{equation}$

1.5. Maprayローカル座標系および姿勢変換

Maprayローカル座標系 $T_\mathrm{MLOCS}$ は下記のように定義されます。

地球上の任意の点 $p_o$ を原点とする
z軸を上方向（地球中心と反対方向）
y軸を北方向（z軸に垂直）
右手系で残りの軸をx軸とする

コーディングについて、mapray.ModelEntity#setPosition() を用いて $p_o$ を指定すると、自動的にMaprayローカル座標系が適用されるようになります。

姿勢変換 $T_\mathrm{attitude}$ は上記座標系へ配置された後で適用されます。現在のバージョンでは Heading, Tilt, Roll でモデルの姿勢変換を行います。

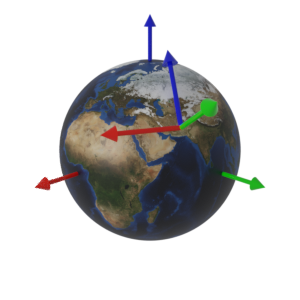
下図は、Maprayローカル座標系、 Heading, Tilt, Roll で回転する方向を示します。（比較のためglTF座標系で回転する方向も示します）

	Maprayローカル座標系	glTF座標系
	Maprayローカル座標系	glTF座標系

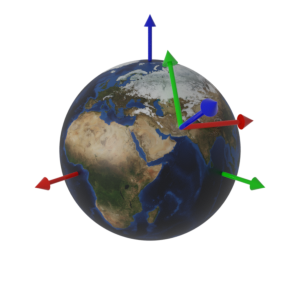Heading	+z軸側から中心を見て時計回り	+y軸側から中心を見て時計回り
Tilt	+x軸側から中心を見て時計回り	+x軸側から中心を見て反時計回り
Roll	+y軸側から中心を見て時計回り	+z軸側から中心を見て時計回り

コーディングについて、mapray.ModelEntity#setOrientation()を用いて姿勢情報を指定します。姿勢情報はmapray.Orientationクラスを用いて表現します。

1.6. 姿勢変換の行列計算

姿勢変換 $T_\mathrm{attitude}$ の詳細な座標変換について説明します。

拡大を示す行列。

$\begin{equation} S = \begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \end{equation}$

+x軸側から中心を見て $\theta$ 時計回りする回転行列。

$\begin{equation} R_x(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & \sin\theta & 0 \\ 0 & -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \end{equation}$

+y軸側から中心を見て $\theta$ 時計回りする回転行列。

$\begin{equation} R_y(\theta) = \begin{pmatrix} \cos\theta & 0 & -\sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ \sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \end{equation}$

+z軸側から中心を見て $\theta$ 時計回りする回転行列。

$\begin{equation} R_z(\theta) = \begin{pmatrix} \cos\theta & \sin\theta & 0 & 0 \\ -\sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \end{equation}$

モデルに対し、下記の順番で演算を行います。

姿勢変換行列 $T_\mathrm{att}$ は下記のようになります。

$\begin{equation} \begin{aligned} T_\mathrm{att} &= R_z(H) \times R_x(T) \times R_y(R) \times S \\ &= \scriptsize \begin{pmatrix} s_x(\sin{R} \sin{T} \sin{H} + \cos{R} \cos{H}) & s_y\cos{T}\sin{H} & s_z (\cos{R} \sin{T} \sin{H} - \sin{R} \cos{H}) & 0 \\ s_x (\sin{R} \sin{T} \cos{H} - \cos{R} \sin{H}) & s_y \cos{T} \cos{H} & s_z (\cos{R} \sin{T} \cos{H} + \sin{R} \sin{H}) & 0 \\ s_x \sin{R} \cos{T} & -s_y \sin{T} & s_z \cos{R} \cos{T} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \end{aligned} \end{equation}$

コーディングについて、mapray.ModelEntity#setOrientation()を用いて姿勢情報を指定すると、上記行列式が自動的に計算されるようになっています。

2. 基本演算

2.1. ベクトル

$\begin{equation} \vec{p} = \begin{pmatrix} p_x \\ p_y \\ p_z \end{pmatrix} \end{equation}$

Maprayでは GeoMath.createVector3 を用いてベクトルを生成します。

const p = GeoMath.createVector3();
// p = [px, py, pz]

2.2. 行列

$\begin{equation} T = \begin{pmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ m_{30} & m_{31} & m_{32} & m_{33} \end{pmatrix} \end{equation}$

Maprayでは GeoMath.createMatrix を用いて行列を生成します。

const m = GeoMath.createMatrix();
// m = [m00, m10, m20, m30, m01, m11, m21, m31, m01, m12, m22, m32, m03, m13, m23, m33]

配列で保存される順番にご注意ください。

2.3. 座標値を行列変換

$\begin{equation} \vec{p_t} = T \vec{p} \end{equation}$

const p = GeoMath.createVector3();
const m = GeoMath.createMatrix();
// p, mに任意の変数を指定する
const result = GeoMath.createVector3([
  m[0]*p[0] + m[4]*p[1] + m[ 8]*p[2] + m[12],
  m[1]*p[0] + m[5]*p[1] + m[ 9]*p[2] + m[13],
  m[2]*p[0] + m[6]*p[1] + m[10]*p[2] + m[14]
]);

2.4. 逆行列

$\begin{equation} T_2 = T^{-1} \end{equation}$

const m = GeoMath.createMatrix();
// p, mに任意の変数を指定する
m2 = GeoMath.inverse_A(m, GeoMath.createMatrix());

3. 座標系

3.1. GOCS座標系

地球中心を原点とする直行座標系

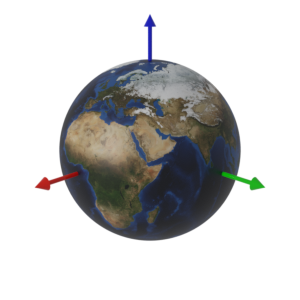
3.2. 緯度・経度座標系

3.3. Maprayローカル座標系

任意の点を原点とする直行座標系

下記のように定義されます。

地球上の任意の点 $p_o$ を原点とする
z軸を上方向（地球中心と反対方向）
y軸を北方向（z軸に垂直）
右手系で残りの軸をx軸とする

この変換行列は、mapray.GeoPoint#getMlocsToGocsMatrix()から取得できます。

Table of Contents